










 Farbfolien
Dichro-Filter
Goboprojektion
Gobotypen
Sicherungsseil
Saveking
Aufhängung
Lightlock
Konventionel
Movinglights
Zubehör
Spiegel
Nachbauten
Farbfolien
Dichro-Filter
Goboprojektion
Gobotypen
Sicherungsseil
Saveking
Aufhängung
Lightlock
Konventionel
Movinglights
Zubehör
Spiegel
Nachbauten


Copyright © Alle Rechte vorbehalten. Made by Herbert Bernstädt: Kontakt | Impressum
Wissenstransfer Veranstaltungstechnik
Profielscheinwerfer, Profiler, spot, Vinjette, Gobo, Elipsenspiegel, Kondensor, Fix,
zoom, Herbert, Bernstädt, Herbert Bernstädt, hbernstaedt, Bernstaedt, Institut,
angewandte, Veranstaltungstechnik, Goboebene, Blendenschieber, nullkraftsockel, Farbrad
Gobo-Projektion bei Profilscheinwerfern
Die Möglichkeit Gobos zu projizieren ist einer der Spezialaufgaben eines Profilscheinwerfers.
Gobos, die im südlicheren Raum auch als Vignetten bezeichnet werden, sind Vorlagen,
die von der Linse des Profilscheinwerfers vergrößert dargestellt werden, indem das
Licht des Lampenhauses durch das Gobo hindurch scheint. Dadurch wird das Licht durch
die Goboflächen abgeschattet, verfärbt oder gar gebrochen, um dann auf eine Fläche,
Szene oder Person scharf oder unscharf abgebildet zu werden. Kurz aus dieser Variablenvielfalt
lässt sich der unermessliche Gestaltungsspielraum mit Gobos erahnen.
Goboposition
In der Regel weisen die Profilscheinwerfer nur ein Goboschacht auf. Aber es gibt
auch Profilscheinwerfer die zwei mehrere Goboslots zur Aufnahme von Gobohaltern bieten.
Man kann zunächst daran denken das man damit die Möglichkeit hat, neben dem Gobo
auch eine Iris einzusetzen, was durchaus dann möglich ist. Jedoch gestalterisch wertvoller
ist hierbei einmal die Möglichkeit der freien Wahl, ob man die Blendenschieber zum
Abschieben eines Teiles im Gobo benötigt und damit der Blendenschieber und das Gobo
scharf abgebildet werden sollen. So könnte z.B. ein Gobo den Text tragen „1.Akt“,
in der Zweiten Zeile „Pause“ und in der dritten Zeite „2.Akt“. Verschiebt man nun
die Oberen und unteren Blendenschieber entsprechend der Zeilen, benötigt man für
drei Texte nur einen Scheinwerfer. Das umrichten der Blendenschieber kann bei den
Umbauten der Akte vorsichtig vorgenommen werden. Anderer seits möchte man einen weichen
Übergang bzw. Abgrenzung erzeugen, aber dennoch das Motiv scharf sehen. Dann ist
eine Goboebene die ein wenig Distanz zur Blendenschieberebene aufweist sehr vorteilhaft.
Nicht vergessen sollte man die Möglichkeit dass man z.B. zwei Gobos gleichzeitig
einsetzt was in der Praxis sehr häufig geschieht. Beispiele hierzu ist typischer
Weise ein Breakup für Laub kombiniert mit einem grünlichen Prismatik oder Colorizer.
Auch hier ist es sinnvoll, z.B. die Palmenstruktur scharf abzubilden, während der
Colorizer unscharf bleibt, denn man will ja nicht die Farbwechsel scharf sehen, bzw.
beim Prismatik ist der Effekt aufgrund seiner unterschiedlichen Tiefenebenen sowieso
sehr interessant.
Gobo wird so nah wie möglich bei den Blendenschiebern platziert
Entweder ist das Gobomotiv scharf oder die Blendenschieber
Goboplazierung gegenüber den Blendenschiebern
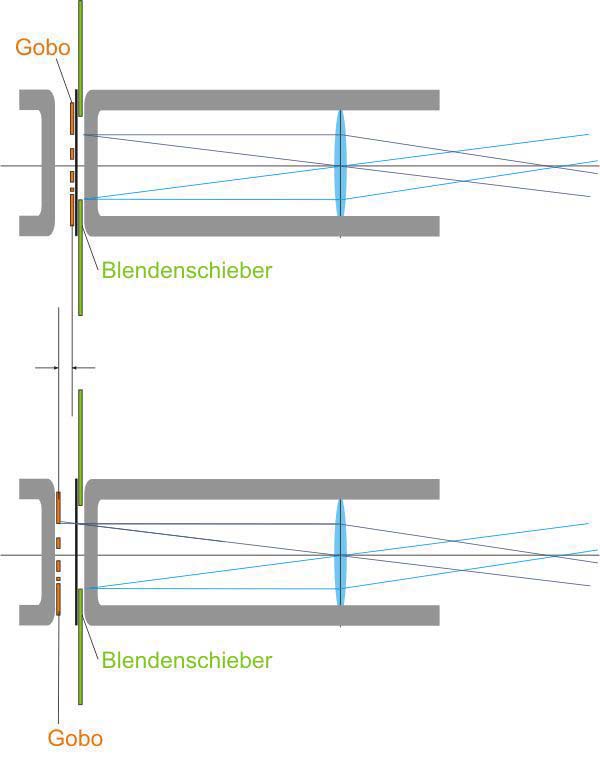



Kleine Positions-verschiebung mit großen Auswirkungen auf die Schärfe.
Motiv und Blendenschieber können weitgehenst gleichzeitig scharf abgebildet werden

Goboprojektion
Für die Erstellung eines Gobos ist es auch wichtig ob das Gobo von vorne auf die
Szenenfläche oder Prospekt projiziert wird, oder als Rückprojektion von hinten auf
eine halbtransparente Folie (wie z.B. eine Operafolie) geworfen wird. Denn nach den
Gesetzen der Optik ist die Projektion mit einer einfachen Linse seitenverkehrt und
auf dem Kopf stehend. Dies kann bei Schriften oder bestimmten Motiven sehr merkwürdig
aussehen. Man kann zwar sagen, das man das Gobo doch jederzeit umdrehen kann. Das
ist richtig wenn es sich um ein Metallgobo handelt welches nicht mit Silikon in den
Gobohalter fixiert wurde. Jedoch bei einem Glasgobo sollte man beachten, das die
beschichtete Seite des Glasgobos vom Leuchtmittel abgewandt sein sollte. Denn damit
wird die thermische Belastung der Beschichtung minimiert.
Weit wichtiger jedoch ist es zu wissen, wie groß mein Gobomotiv an die Wand geworfen
wird. Einmal kann man auf praktische Weise die benötigte Imagegröße oder den Abstrahlwinkel
des Scheinwerfers ermitteln. Sehr praktisch ist dabei ein „Fadenkreutz“ oder Raster-Gobo
oder auf englisch das „Line up Grid“. Dieses Gobo ist in 1 cm Raster aufgeteilt,
welches noch in o,5 cm Hilfslinien und 1mm Marken unterteilt ist. Darüber hinaus
sind noch die Ziffern in eins bis drei abgebildet, so dass man mit diesem Gobo auch
gleichzeitig die Seitenverkehrtheit und auf den Kopf stehend Verdrehung der Optik
überprüfen kann, bzw. einen solchen Fehler von vornherein ausschließt. Dieses Gobo
ist als Standardgobo bei fast allen Goboherstellern in den A-Size und B-Size Größen
erhältlich und sollte bei keinem Lichtgestallter der mit Goboprojektionen arbeitet,
als Kontroll- und Erstellungshilfsmittel fehlen.
Raster-Gobo im Einsatz bei Frontalprojektion
Seitliche Projektion auf die gleiche Fläche weist natürlich eine Verzeichnung auf.
Hilfsmittel „Raster-Gobo“



Nun hat man aber oft nicht die Möglichkeit vom Rang das Gobo frontal auf den Rücksetzer
bzw. Prospekt zu werfen, sondern muss von der Seite aus Projizieren. Auch hier kann
das „Fadenkreutz“ – Gobo weiterhelfen. Wie hier im Beispielbild soll z.B. ein Firmenlogo
die Leinwand vollflächig abdecken. Nun kann man anhand des Rastergobos die Ecken
der Leinwand mit der Position auf dem Gobo festlegen. Auch hier sei der modernen
Computertechnik dank, denn wenn man nun das Fimenlogo als Vorlage hat, kann man mit
einem guten Bildbearbeitungsprogramm das Orginalbild verzerren, indem man die Ecken
des Logos auf die ermittelten Positionen der Schrägprojektion überträgt und damit
das Bild verzeichnet.
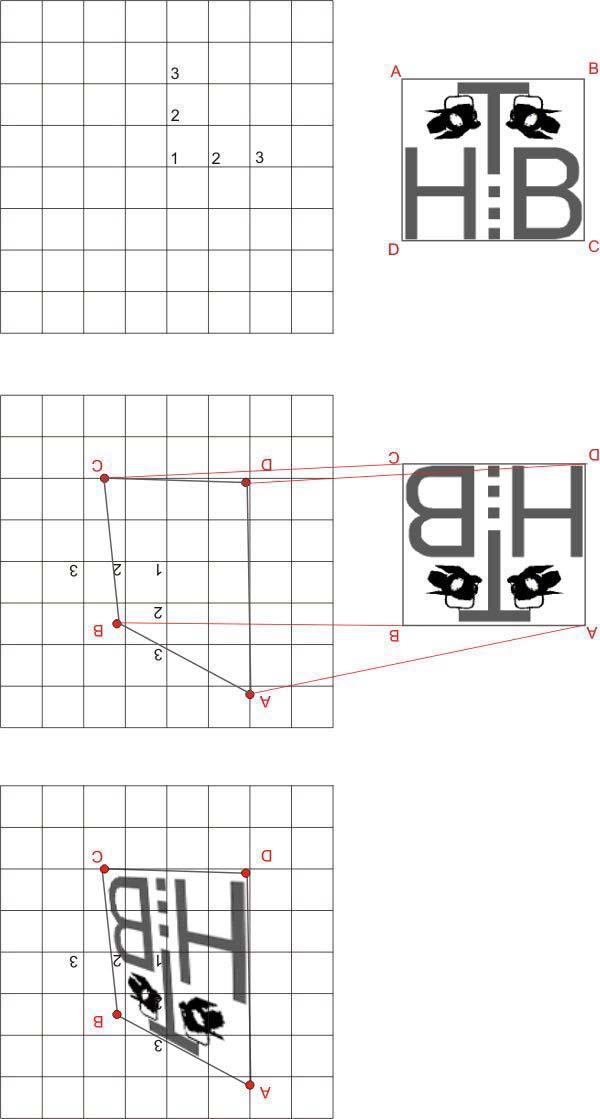
Ermittlung der Goboverzerrung wegen Schrägprojektion, dabei werden die Eckpunkte
aus der Rasterprojektion in die Zeichenskizze übertragen und die Ecken des Logobildes
auf die Punkte gesetzt, wobei das Bild entsprechen verzerrt wird.
Jetzt wissen wir, wie das Gobo bei Schrägprojektion verzeichnet werden muss. Aber
wenn wir es in einer bestimmten Größe in einer bestimmten Entfernung projizieren
wollen, benötigen wir noch den benötigten Abstrahlwinkel des Scheinwerfers. Diesen
erhält man aus den Photometrischen Datenblatt des Scheinwerferherstellers. Auf der
anderen Seite kann man aber grob davon ausgehen, das die Angabe bei einem, auf den
äußeren Rand scharf gezogenen Profilscheinwerfer, der Halbertswinkel beinahe identisch
mit den 1/10 Gradswinkel. Mann könnte nun anhand der Brennweite der Linsen und der
Motivgröße mathematisch die exakte Projektionsgröße in jeder Entfernung berechnen.
Nehmen wir z.B. eine Gobo mit der Größe A (A-Size) an, dann ist der Bilddurchmesser
mit 75mm festgelegt worden. Das Gobo im Abstand der doppelten Brennweite zur Linse
hat folglich eine gleich großes Projiziertes Bild in ebenfalls doppelter Brennweite
zur Folge, jedoch werden die Brennweiten sehr selten bei Scheinwerfern angegeben,
sondern nur die Abstrahlwinkel. In der Regel reicht für uns dieser grobe Wert und
man kann nun wie folgt aus dem Abstrahlwinkel mit Hilfe der Trigonometrie die zu
erwartenden Projektionsgröße errechnen. Betrachtet man die folgende Zeichnung, so
wird man schnell das rechtwinklige Dreieck erkennen. Demnach ist der Tangens von
Alpha gleich dem Verhältnis aus Gegenkathete zur Ankathete. Für diejenigen, die kein
Programm, zur Berechnung der Lichtfeldgröße, öffnen wollen, haben wir eine Übersichtstabelle
angefügt, die die einfache Zuordnung von Abstrahlwinkel, Entfernung und Lichtfeldgröße
wiedergibt. Für diejenigen, die sich Ihre eigne Tabelle erstellen wollen oder direkt
die Werte neu berechnen wollen folgt hier ein kleiner Exkurs in Excel. Der Projektionsdurchmesser
ist ein Formelfeld das die Berechnete Formel wiedergibt. Die Formel in dem Feld muss
lauten: =TAN(($A15/2)*PI()/180)*M$2*2
Zur Erläuterung, das $-Zeichen steht dafür das die Formel immer auf dieses Feld-Koordinate
verweist, auch wenn man die Formel kopiert. Damit lässt sich die Formel sehr schnell
in große Flächen kopieren und der Bezug stimmt trotzdem, denn sonst macht Excel automatisch
ein Offset, so wie wir Ihn bei der zweiten Feldkoordinate auch benötigen. $A bedeutet
also immer Spalte A, während 15 die Zeile in der nächsten Zeile zu 16 macht.
Dann teilen wir den Abstrahlwinkel, der vom Hersteller angegeben, wird durch zwei,
womit wir dann ein rechtwinkliges Dreieck erhalten ($A15/2).
Und nun zum eigentlichen Knackpunkt, der Berücksichtigung das 1° = Phi / 180 rad
ist, erweitert sich so die Formel in Excel zu ($A15/2)*PI()/180.
Nun kann man den Tangens von Alpha bilden mit TAN(($A15/2)*PI()/180) und multipliziert
das nun mit dem Abstand der Projektion *M$2.
Damit erhalten wir aber nun die Gegenkathete unseres rechtwinkligen Dreiecks welches
dem Radius des Lichtkreises entspricht. Folglich multiplizieren wir den Radius mit
2 (M$2*2) und voila, damit haben wird den Durchmesser bestimmt. Die Formel nun sachgerecht
umgestellt ermöglicht uns nun bei zwei bekannten Größen nun die dritte unbekannte
ebenfalls zu berechnen.
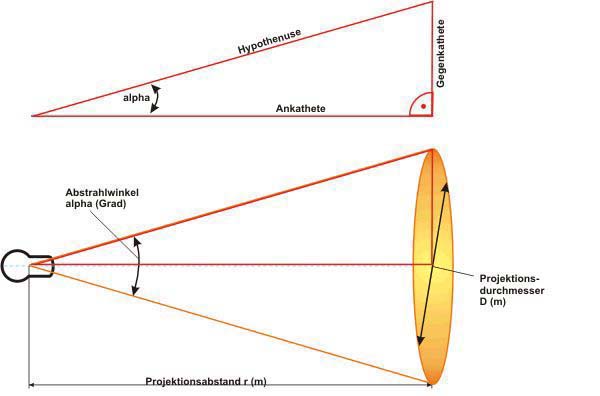
Berechnung des Abstrahlwinkels
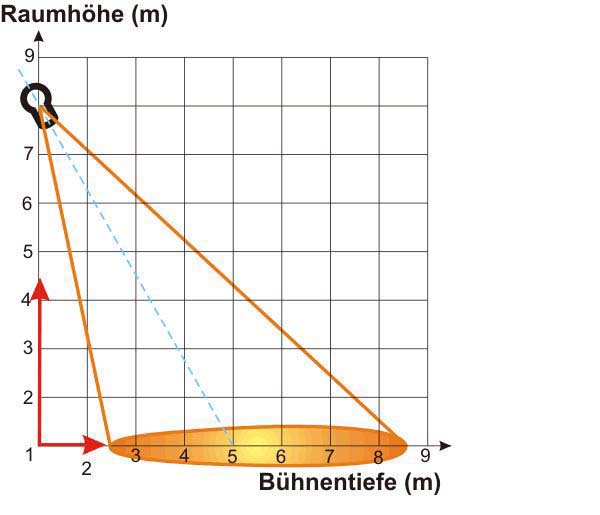
Jedoch sind diese Werte nur bei frontaler Projektion gültig. In der Praxis jedoch
wird meist schräg projiziert, und jeder weiß, das man statt einen Kreis ein Oval
erhält. Im folgenden Bild lässt sich das auch leicht erkennen warum das so ist. Auch
hier kann man die Trigometrie anwenden. Leuchtet der Profilscheinwerfer in 8m Höhe
in einem Winkel von 32° auf die Szenenfläche, so ist das Zentrum des Lichtes in 5m
Bühnentiefe zu finden, frei nach dem rechtwinkligen Dreieck und Tangens(alpha) ist
gleich 5m Bühnentiefe zur 8m Bühnenhöhe. Bei einem Abstrahlwinkel von 30° des Scheinwerfers,
ist demnach der Winkel nur noch 17° wenn man das rot angedeutete Dreieck betrachtet,
da 32° Winkelposition des Scheinwerfers minus halben Abstrahlwinkel gerechnet wurde.
Somit ergibt sich ein erstes Auftreffen des Lichtkegels in 2,45m nach Tangens von
17° mal der Scheinwerferhöhe. Ebenso erhält man den weitesten Ausläufer aus Tangens
von 47° und ebenfalls der 8m Scheinwerferhöhe mit 8,6m.
reale Flächenprojektion
Betrachten wir ein ausgeleuchtetes Bühnenbild mit konventionellen Scheinwerfern,
so ist das Bild, einmal abgesehen von Überblendungen sehr statisch. Um die Illusion
eines heißen Passatwind an einer Palmenbewachsenen Küstenstreifen zu erlangen, könnte
man Palmenblätter sehr schräg auf ein Vorhang projizieren und dann diesen Vorhang
mit einen Ventilator in Bewegung versetzen. Durch die Bewegung des Vorhanges fangen
dann die Projektionen auf der dem Vorhang an zu bewegen. Somit kann man sehr rudimentär
ein wenig mehr Dynamik in das statische konventionelle Szenenbild bringen. Natürlich
könnte man solch Palmenblätter projizierenden Scheinwerfer auf sehr gut schwingende
um nicht wacklige Aufhängungen befestigen. Ein leichtes drankommen und die Palmenwedel
werden ebenfalls wackeln, eben so wie von Wind. Aber diese Art der Bewegung ist sehr
Personalintensiv, und so hat man andere Möglichkeiten geschaffen um dynamisches Licht
mit Konventionellen Scheinwerfern zu realisieren. Es ist nahe liegend das Gobo in
dem Scheinwerfer zu bewegen, was auch mit dem Goborotator realisiert wird. Goborotatoren
können ein oder zwei Gobos aufnehmen. Dabei kann ein Gobo je nach Ausführung des
Goborotator in eine oder beide Richtungen in verschiedenen Geschwindigkeiten drehen.
Je nach Ausführung kann die Drehgeschwindigkeit nur am Gerät selbst oder fernsteuerbar
über DMX 512 erfolgen. Nun kann der Vorhang mit entsprechender Drehgeschwindigkeit
und Goboauswahl der typische Effekt realisieren wie Lichtreflexionen von einer Wasseroberfläche
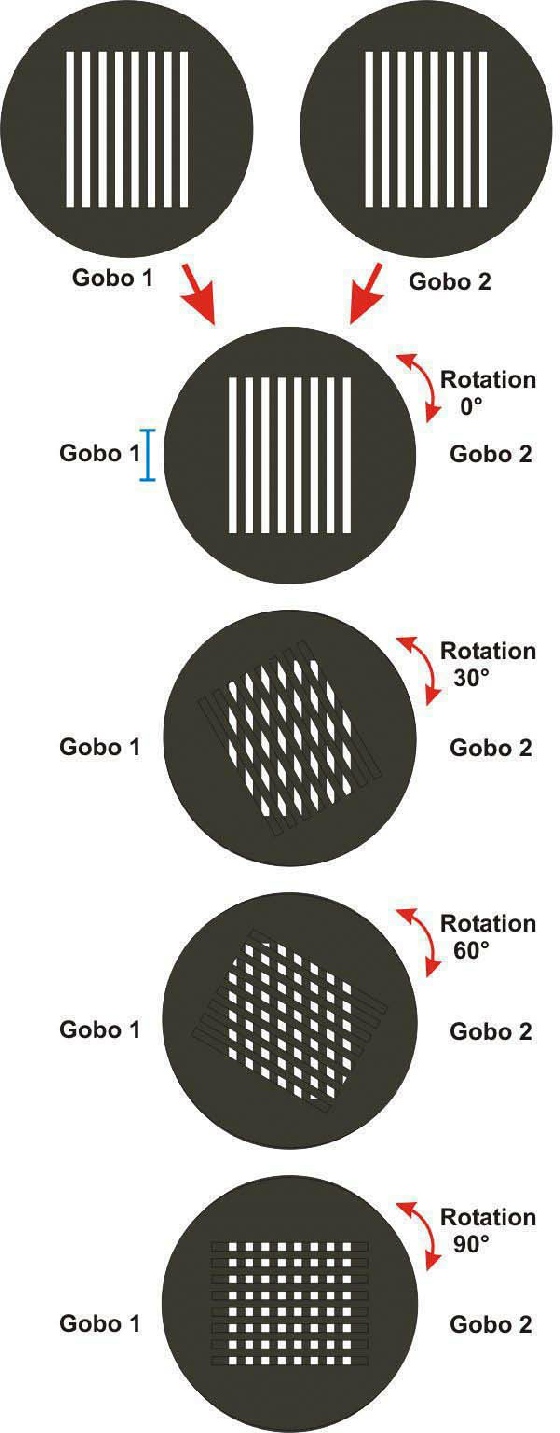
an die Schwimmbadwand. Werden fein strukturiertem Schwarz Weiß Linien oder Raster
als Gobos eingesetzt die gegen einander drehen, kann der Moiré-Effekt interessant
wirken. Unter Moiré-Effekt versteht man durch Überlagerung von Rastern oder Linien
die die Entstehung neuer Linien bzw. Formen hervorrufen. Natürlich spielt bei Goboratatoren
auch die Qualität der Mechanik eine große Rolle. Wenn Gobos bei der Rotation verrücken
können, oder die Langsame Geschwindigkeit anfängt zu zuckeln oder erst gar kein langsame
Geschwindigkeiten möglich sind, ist das natürlich nicht so günstig.
Gobo Rotation
Positionierung des Goborotator im Goboschacht
(Quelle: Lightpower)
Zwei Gobos, die gegeneinander rotieren können. Beispiel für den Moiré-Effekt.

War bei der Goborotation die Drehachse im Zentrum des Gobos gelegen, ist bei der
Effektrotation die Drehachse außerhalb des durchleuchteten Gobomotivs. Die wendet
man sehr gerne bei Wolken an, denn diese ziehen je nach Windrichtung immer von einer
Seite zur anderen. Bei einem nur in sich rotierenden Gobo das vollständig mit Licht
durchschienen wird, würde das ein in sich drehende Wolke darstellen was allenfalls
für ein Tornado zutrifft. Also muss die Achse außerhalb liegen, und nur ein kleiner
Teil wird vom Licht durchschienen, somit erfolgt eine unendliche Bewegung von einer
Seite weg. Betrachtet man die Wolken, so können diese auch unscharf wiedergegeben
werden. Genauso verhält sich das mit Wasser oder Feuer, was nicht immer scharfe Konturen
aufweist. Deshalb hatte man schon früh damit begonnen sehr einfach diesen Rotationseffekt
vor den Scheinwerfer zu platzieren.
Effekt Rotation
Wolkeneffekt-goboscheibe in rotation
Scharfe Abbildung des einer Wolkeneffektgobos cheibe


Oftmals ist aber durch das Verlassen der Abbildungsebene und dem Einsetzen des Effektrades
vor dem Scheinwerfer die Abbildung doch zu unscharf. Dann muss man diesen Effekt
in die Goboebene bringen. Es gibt nur sehr begrenzt Lösungen für Scheinwerfer für
eine solche Effekteinheit die für die Goboebene angefertigt werden. Man kommt oft
dahin, das man dafür einen eignen Profilscheinwerfer verwendet, bzw. eine konventionelles
Linsenscheinwerfergehäuse, dem man die Rotationseinheit vorsetzt und dann die abbildendegebende
Optik darauf anschließt.
Gobohalter
Wie wir aus den vorausgegangenen Abschnitt schon erfahren haben ist die Befestigung
gerade von Glasgobos aufgrund der Temperaturverspannung nicht unkritisch. Bei Metallgobos
möchte man mit dem Gobohalter versuchen die Wärmeverwerfungen möglichst klein zu
halten. In den folgenden Bildern sind zwei unterschiedliche Varianten zu sehen. Einmal
wird über die gesamte äußere Haltefläche ein Rahmen über das Gobo gelegt, welches
mit Federkraft angedrückt wird. Bei der anderen Lösung, und hier bitte das Gobo mit
dem Firmennamen nicht im Zusammenhang mit dem Gobohalter bringen, sind nur drei Haltenasen
vorhanden und man muss das Gobo stark biegen, um es in die Halterungen einzuführen.
Dabei wird deutlich dass dieser Gobohalter nur Metallgobos aufnehmen kann. Aber es
werden heute immer mehr Gobohalter geliefert die sowohl die dickeren Glasgobos wie
auch die dünnen Metallgobos aufnehmen können.
Aufwendiger Gobohalter mit umlaufenden Andruckring und Feder-mechanismus


Einfacher Gobohalter, Einsetzen nur mit starken biegen möglich.
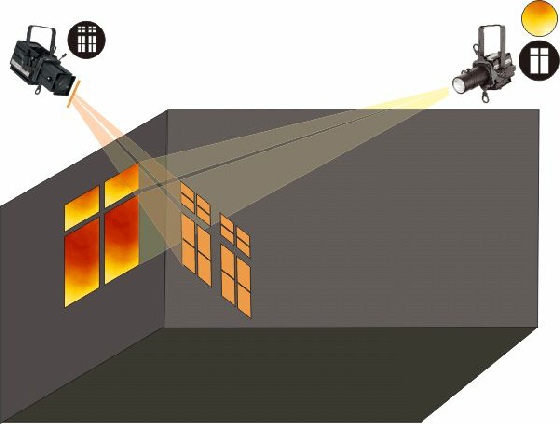
Typische Anwendung
für eine Fenstersimulation
Wem das Berechnen via Exceltabelle zu aufwendig ist, kann auch die nebenstehenden
PDF herunterladen, einer berechneten Tabelle für Projektionsgröße in Abhängigkeit
von Abstand und Winkel.


































